Theoretical background
In order to analyse the clustering of particles, the second reduced moment K function and the pair-correlation function (PCF) were used (Stoyan et al., 1995). The K function is the number of gold particles (or points) at distances shorter than a given distance from a typical particle divided by the average density of these particles (see Fig. 1). PCF is a ratio of the density of gold particles at a given distance from a typical particle to the average density of these particles. Thus it is in principle possible to obtain PCF from the K function by differentiation using the following formula (Stoyan et al., 1995):
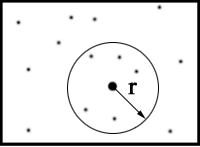
Fig. 1
FIG. 1. A graphical representation of the evaluation of K and cross K functions. K function is the ratio of the number of gold particles (points) at distances shorter than a given distance r (i.e. the points which are inside the circle with the radius r) from a typical particle of the same type (large point in the center of the circle) to the average density of these particles (here - the total number of particles in the frame divided by the area of this frame). In the case of the cross K function, the large point in the center of the circle is a typical particle of the 2nd type while the remaining points are the particles of the 1st type.
Similarly, we evaluated the pair-crosscorrelation function (PCCF) as the ratio of the density of particles of the 1st type at the given distance from a typical particle of the second type to the average density of the particles of the 1st type. For PCCF and cross-K function the same relationship holds as for PCF and K function (see formula above). The pair- (cross)correlation functions are useful for exploratory analysis, while the K functions - for statistical testing (Stoyan et al., 1995). The exploratory analysis provides one with information if the clustering or colocalization is present, and if so at what distances. This information can be then used in more detailed confirmatory analysis, especially for setting the appropriate ranges of distances that are to be tested. Inappropriately low range might cause an omission of significant clustering/colocalization at distances longer than set. In contrast, too high range - much larger than the typical size of clusters - would cause a low spatial resolution of the test.
The above functions were calculated from pooled data from all images of nucleoplasm in each experimental group. Let N be the number of images of size a x b. Let n
 ,i
be the number of 10 nm
particles in the image number i; similarly, let
n
,i
be the number of 10 nm
particles in the image number i; similarly, let
n ,i
be the number of 5 nm
particles in image number
i; i=1..N. Then density of j-th labelling
,i
be the number of 5 nm
particles in image number
i; i=1..N. Then density of j-th labelling 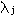 (j=1 or j=2 in case of 10 nm or 5 nm gold particles,
respectively) can be estimated as
(j=1 or j=2 in case of 10 nm or 5 nm gold particles,
respectively) can be estimated as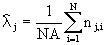
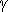 of the window (Ripley, 1988).
In order to obtain this parameter, a rectangle with sides a and b (which corresponds to an image)
was shifted by distance r in all directions from 0 to 2
of the window (Ripley, 1988).
In order to obtain this parameter, a rectangle with sides a and b (which corresponds to an image)
was shifted by distance r in all directions from 0 to 2 , and the area of intersections between
the original rectangle and the shifted ones was evaluated (see Fig. 2B).
, and the area of intersections between
the original rectangle and the shifted ones was evaluated (see Fig. 2B).

Fig. 2
FIG. 2. Correction of the boundary effect using geometric window covariogram. (A) The probability that one gold particle from the pair is situated outside of the window (image) increases with an increase of the distance r at which the colocalization/clustering is evaluated. (B) This negative influence, called boundary effect, may be corrected using the geometric covariogram
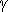 of the window. To obtain this parameter, a rectangle with sides a and b is
shifted by distance r in all directions (
of the window. To obtain this parameter, a rectangle with sides a and b is
shifted by distance r in all directions ( angle ranges from 0 to
2
angle ranges from 0 to
2 ), and the areas of
intersections between the original rectangle and the shifted ones (grey-coloured area) were
measured. The geometric window covariogram
), and the areas of
intersections between the original rectangle and the shifted ones (grey-coloured area) were
measured. The geometric window covariogram 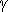 (r) equals to the average area of the
intersections; a and b equal to the length of the sides of the window.
(r) equals to the average area of the
intersections; a and b equal to the length of the sides of the window.
The average area of intersections which corresponds to the geometric window covariogram
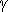 (r) can be then calculated for
r < min (a,b) accordingly:
(r) can be then calculated for
r < min (a,b) accordingly: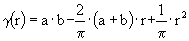
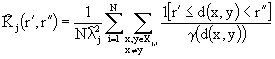
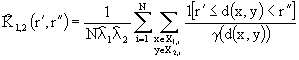
 d(x,y)< r'' means that point y is lying inside the sector created with circles of
the radius r' and r'' which have center in the point x (see Fig. 3).
d(x,y)< r'' means that point y is lying inside the sector created with circles of
the radius r' and r'' which have center in the point x (see Fig. 3).
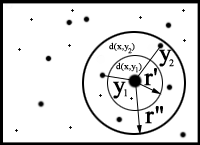
Fig. 3
FIG. 3. Illustration for the estimation of the bottom censored K and cross K functions for particles of one or two types, respectively. Let x, y
 and
y
and
y will be the particles of the same
type. In both cases d(x,y
will be the particles of the same
type. In both cases d(x,y ) and d(x,y
) and d(x,y ) (distances between points x and y
) (distances between points x and y and x and y
and x and y ) fulfil
the condition r'
) fulfil
the condition r'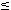 d(x,y)< r''. Any point yn will be taken into account for the evaluation of the
bottom censored K function only if it is laying inside the sector, delimited by the circles of the
radius r' and r'' with a common center in the point x. In case of the evaluation of the bottom
censored cross K function, the point x will be a gold particle of one type while points yn will
be the gold particles of the other type. Thus the colocalization/clustering at a specified range
of distances can be evaluated by comparing the densities of particles yn inside the sector to the
average density of these particles.
d(x,y)< r''. Any point yn will be taken into account for the evaluation of the
bottom censored K function only if it is laying inside the sector, delimited by the circles of the
radius r' and r'' with a common center in the point x. In case of the evaluation of the bottom
censored cross K function, the point x will be a gold particle of one type while points yn will
be the gold particles of the other type. Thus the colocalization/clustering at a specified range
of distances can be evaluated by comparing the densities of particles yn inside the sector to the
average density of these particles.
Thus the expression "1[condition]" is for indicator function; it has value 1 if the condition is fulfilled and 0 otherwise. Similarly, we estimate
 and
and 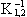 which are the integrals (from r' to r'') of pair-correlation and pair-crosscorrelation functions (PCF and PCCF, Stoyan et al., 1995) respectively
as:
which are the integrals (from r' to r'') of pair-correlation and pair-crosscorrelation functions (PCF and PCCF, Stoyan et al., 1995) respectively
as: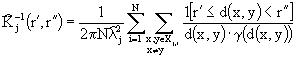
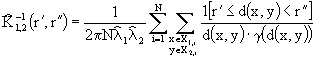
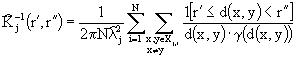
and
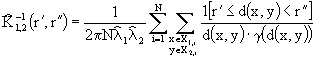

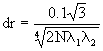
References
Barnard, G. (1963) Contribution to discussion of Bartlett. Journal of Royal Statistical Society B25, 294.
Ripley, B. D. (1980) Spatial statistics. John Wiley & Sons, New York, Chichester, Brisbane, Toronto
Ripley, B. D. (1988) Statistical inference for spatial processes. Cambridge University Press, Cambridge, New York, New Rochelle, Melbourne, Sydney
Stoyan, D., Kendall, W. S., and Mecke, J. (1995) Stochastic geometry and its applications. John Wiley & Sons, Chichester, New York, Brisbane, Toronto, Singapore
